Shear modulus
|
|
|
| SI symbol: | G |
| SI unit: | gigapascal |
| Derivations from other quantities: | G = Ο / Ξ³ |
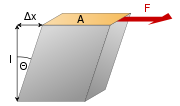
In materials science, shear modulus or modulus of rigidity, denoted by G, or sometimes S or ΞΌ, is defined as the ratio of shear stress to the shear strain:[1]
where
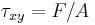 = shear stress;
= shear stress;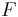 is the force which acts
is the force which acts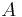 is the area on which the force acts
is the area on which the force acts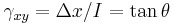 = shear strain;
= shear strain;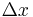 is the transverse displacement
is the transverse displacement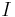 is the initial length
is the initial length
Shear modulus is usually expressed in gigapascals (GPa) or thousands of pounds per square inch (ksi).
Contents |
Explanation
| Material | Typical values for shear modulus (GPa) (at room temperature) |
|---|---|
| Diamond[2] | 478. |
| Steel[3] | 79.3 |
| Copper[4] | 44.7 |
| Titanium[3] | 41.4 |
| Glass[3] | 26.2 |
| Aluminium[3] | 25.5 |
| Polyethylene[3] | 0.117 |
| Rubber[5] | 0.0006 |
The shear modulus is one of several quantities for measuring the stiffness of materials. All of them arise in the generalized Hooke's law:
- Young's modulus describes the material's response to linear strain (like pulling on the ends of a wire),
- the bulk modulus describes the material's response to uniform pressure, and
- the shear modulus describes the material's response to shearing strains.
The shear modulus is concerned with the deformation of a solid when it experiences a force parallel to one of its surfaces while its opposite face experiences an opposing force (such as friction). In the case of an object that's shaped like a rectangular prism, it will deform into a parallelepiped. Anisotropic materials such as wood and paper exhibit differing material response to stress or strain when tested in different directions. In this case, when the deformation is small enough so that the deformation is linear, the elastic moduli, including the shear modulus, will then be a tensor, rather than a single scalar value.
Waves
In homogeneous and isotropic solids, there are two kinds of waves, pressure waves and shear waves. The velocity of a shear wave, 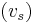 is controlled by the shear modulus,
is controlled by the shear modulus,
where
- G is the shear modulus
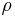 is the solid's density.
is the solid's density.
Shear modulus of metals
In homogeneous and isotropic solids, there are two kinds of waves, pressure waves and shear waves The shear modulus of metals measures the resistance to glide over atomic planes in crystals of the metal. In polycrystalline metals there are also grain boundary factors that have to be considered. In metal alloys, the shear modulus is observed to be higher than in pure metals due to the presence of additional sources of resistance to glide.
The shear modulus of metals is usually observed to decrease with increasing temperature. At high pressures, the shear modulus also appears to increase with the applied pressure. Correlations between the melting temperature, vacancy formation energy, and the shear modulus have been observed in many metals[9].
Several models exist that attempt to predict the shear modulus of metals (and possibly that of alloys). Shear modulus models that have been used in plastic flow computations include
- the MTS shear modulus model developed by [10] and used in conjunction with the Mechanical Threshold Stress (MTS) plastic flow stress model [11][12]).
- the Steinberg-Cochran-Guinan (SCG) shear modulus model developed by [13] and used in conjunction with the Steinberg-Cochran-Guinan-Lund (SCGL) flow stress model.
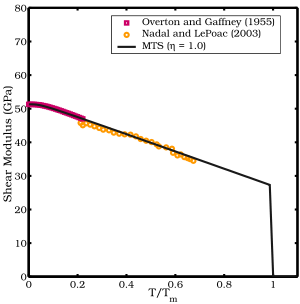
- the Nadal and LePoac (NP) shear modulus model [8] that uses Lindemann theory to determine the temperature dependence and the SCG model for pressure dependence of the shear modulus .
MTS Shear Modulus Model
The MTS shear modulus model has the form
where 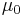 is the shear modulus at 0K, and
is the shear modulus at 0K, and 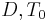 are material constants.
are material constants.
SCG Shear Modulus Model
The Steinberg-Cochran-Guinan (SCG) shear modulus model is pressure dependent and has the form
where, 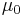 is the shear modulus at the reference state(
is the shear modulus at the reference state(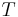 = 300 K,
= 300 K, 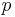 = 0,
= 0, 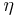 = 1),
= 1), 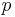 is the pressure, and
is the pressure, and 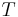 is the temperature.
is the temperature.
NP Shear Modulus Model
The Nadal-Le Poac (NP) shear modulus model is a modified version of the SCG model. The empirical temperature dependence of the shear modulus in the SCG model is replaced with an equation based on Lindemann melting theory. The NP shear modulus model has the form
where
and 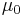 is the shear modulus at 0 K and ambient pressure,
is the shear modulus at 0 K and ambient pressure, 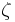 is a material parameter,
is a material parameter, 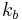 is the Boltzmann constant,
is the Boltzmann constant, 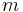 is the atomic mass, and
is the atomic mass, and 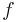 is the Lindemann constant.
is the Lindemann constant.
See also
- Shear strength
- Dynamic modulus
- Hooke's law
- Impulse excitation technique
References
- β IUPAC Gold Book internet edition: "shear modulus, G".
- β McSkimin, H.J.; Andreatch, P. (1972). "Elastic Moduli of Diamond as a Function of Pressure and Temperature". J. Appl. Phys. 43: 2944β2948. doi:10.1063/1.1661636.
- β 3.0 3.1 3.2 3.3 3.4 Crandall, Dahl, Lardner (1959). An Introduction to the Mechanics of Solids. McGraw-Hill.
- β Material properties
- β Spanos, Pete (November 2003). "Cure system effect on low temperature dynamic shear modulus of natural rubber". Rubber World. http://www.thefreelibrary.com/Cure+system+effect+on+low+temperature+dynamic+shear+modulus+of...-a0111451108.
- β Shear modulus calculation of glasses
- β Overton, W. C., Gaffney, J., 1955. Temperature variation of the elastic constants of cubic elements. I. Copper. Physical Review 98(4), 969--977.
- β 8.0 8.1 Nadal, M.-H., Le Poac, P., 2003. Continuous model for the shear modulus as a function of pressure and temperature up to the melting point: analysis and ultrasonic validation. J. Appl. Phys. 93 (5), 2472--2480.
- β March, N. H., (1996), Electron Correlation in Molecules and Condensed Phases (Physics of Solids and Liquids), Springer.
- β Varshni, Y. P., 1970. Temperature dependence of the elastic constants. Physical Rev. B 2(10), 3952--3958.
- β Chen, S. R., Gray, G. T., 1996. Constitutive behavior of tantalum and tantalum-tungsten alloys. Metall. Mater. Trans. A 27A, 2994--3006.
- β Goto, D. M., Bingert, J. F., Chen, S. R., Gray, G. T., Garrett, R. K., 2000. The mechanical threshold stress constitutive-strength model description of HY-100 steel. Metallurgical and Materials Transactions A 31A, 1985--1996.
- β Guinan, M. W., Steinberg, D. J., 1974. Pressure and temperature derivatives of the isotropic polycrystalline shear modulus for 65 elements. J. Phys. Chem. Solids 35, 1501--1512.
|
|||||
| Conversion formulas | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Homogeneous isotropic linear elastic materials have their elastic properties uniquely determined by any two moduli among these, thus given any two, any other of the elastic moduli can be calculated according to these formulas. | ||||||||||
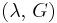 |
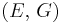 |
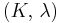 |
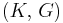 |
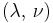 |
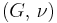 |
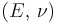 |
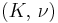 |
 |
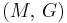 |
|
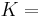 |
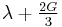 |
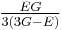 |
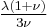 |
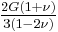 |
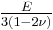 |
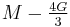 |
||||
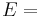 |
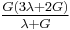 |
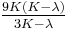 |
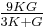 |
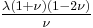 |
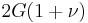 |
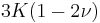 |
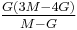 |
|||
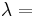 |
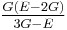 |
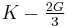 |
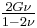 |
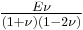 |
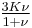 |
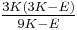 |
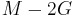 |
|||
 |
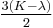 |
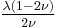 |
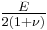 |
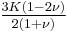 |
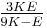 |
|||||
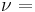 |
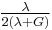 |
 |
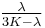 |
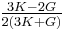 |
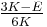 |
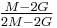 |
||||
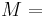 |
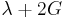 |
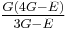 |
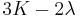 |
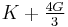 |
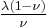 |
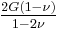 |
 |
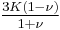 |
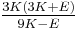 |
|
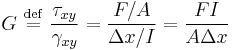
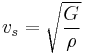
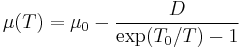
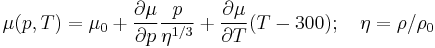
![\mu(p,T) = \frac{1}{\mathcal{J}(\hat{T})}
\left[
\left(\mu_0 + \frac{\partial \mu}{\partial p} \cfrac{p}{\eta^{1/3}} \right)
(1 - \hat{T}) + \frac{\rho}{Cm}~k_b~T\right]; \quad
C := \cfrac{(6\pi^2)^{2/3}}{3} f^2](/I/89204b4da48ab97c79128bf081d3ca6c.png)
![\mathcal{J}(\hat{T}) := 1 + \exp\left[-\cfrac{1+1/\zeta}
{1+\zeta/(1-\hat{T})}\right] \quad
\text{for} \quad \hat{T}:=\frac{T}{T_m}\in[0,1+\zeta],](/I/2e5e7f05e822a254c69e0d78f7ffd8ee.png)
 ) β’
) β’ 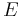 ) β’ LamΓ©'s first parameter (
) β’ LamΓ©'s first parameter (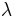 ) β’ Shear modulus (
) β’ Shear modulus (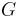 ) β’
) β’ 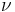 ) β’ P-wave modulus (
) β’ P-wave modulus (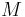 )
)